Domain Decomposition
Parallel programs must break down something to distribute among the different processes or threads. In our previous discussion we talked generally about task parallelism and data parallelism, but we have seen few concrete examples applied to programming. One of the most common parallelisms is a form of data decomposition called domain decomposition. This is typically used for data that can be represented on some form of grid. We break the grid down into subgrids, and assign each subgrid to a process rank. There is no hard and fast rule for numbering the subgrids and usually multiple options are possible.
For a concrete example, consider a two-dimension grid of points, with a function defined at each point. Consider a simple case of four processes. Two obvious possible rank assignments are left-to-right or cyclic.
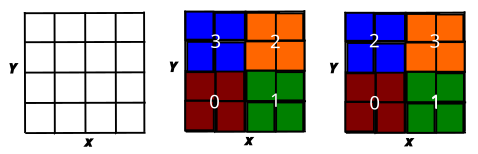
How to assign the numbers to the subdomains may depend on the problem. MPI provides some utilities that may help with this, but using them requires creating a new communicator group, which we have not discussed, so for now we will do our ordering manually.
Let us consider the “brute force” maximum problem of Project Set 1. In that example, we randomly evaluated a function over a two-dimensional set of $x$ and $y$ values and used gathers to find an approximation to the value and location of the maximum. Another approach is to divide up the grid and perform our random searches independently over each subgrid, then collect results from each subdomain and compare them to find the maximum and its location.
A little thought and experimentation suggests that the simplest way to map ranks to subdomains is to divide the overall grid into $np$ regions, where $np$ is the number of processes, then label each domain by row and column number, starting the counts from $0$. The number of processes must be a multiple of two integers. In our example we will assume we will use a perfect square, so our grid is $\sqrt{np}$ on each side. This is not required, but if a more general breakdown is desired, the program must be provided the number of rows and columns and the number of processes should be confirmed to be $n_{rows} \times n_{cols}$. Each process rank then computes its location in the grid according to
col_num=rank%ncols
row_num=rank//nrows
using Python syntax. The local column number is the remainder of the rank divided by the number of columns, and the local row number is the integer division of the rank by the number of rows. This layout corresponds to a rank assigment such as the following, for nine processes:
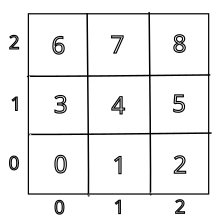
With this decomposition, each rank evaluates the same number of random points, so this is an example of weak scaling.
Exercise
If you have not worked the example from Project Set 1, download the sample serial codes referenced there.
Implement the domain decomposition method to solve this problem. The basic method does not take too many lines of code. The example solutions also check that the number of processors is a perfect square, but you may assume that for a first pass. For correct statistical properties you should also attempt to use different random seeds on different ranks. Be sure not to end up with a seed of $0$ on rank $0$.
Hint: From $xlo$, $xhi$, and $ncols$, compute the increment for each block in $x$ values. Repeat for $y$ values using $ylo$, $yhi$, and $nrows$. Compute the location in rows and columns for each rank
col_num=rank%ncols
row_num=rank//nrows
You can now compute the starting and ending $x$ and $y$ values for each rank.
Example Solutions
C++
#include <iostream>
#include <iomanip>
#include <string>
#include <sstream>
#include <random>
#include <cmath>
#include "mpi.h"
using namespace std;
#define urand ((double)rand()/(double)RAND_MAX);
float surface(float x, float y) {
float pi=4.0*atan(1.0);
float mu1, mu2, sig1, sig2;
float a, b;
float z1, z2;
mu1=sqrt(2.0);
mu2=sqrt(pi);
sig1=3.1;
sig2=1.4;
z1=0.1*sin(x)*sin(x*y);
a=pow((x-mu1),2)/(2*pow(sig1,2));
b=pow((y-mu2),2)/(2*pow(sig2,2));
z2=exp(-(a+b))/(sig1*sig2*sqrt(2.0*pi));
return z1+z2;
}
int main(int argc, char **argv) {
float xval, yval, zval;
int nprocs, rank;
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
// For this example we'll use perfect square nprocs. Otherwise we have
// to tell it how to divide up the processes into rows and columns.
float rows=pow(nprocs,0.5);
int nrows=int(rows);
int ncols=nrows;
int nsamps;
bool shutdown=false;
if (rank==0) {
if ( argc != 2 ) {
cout <<"Usage: number of samples to test\n";
shutdown=true;
}
else if ( pow(int(rows+0.5),2) != nprocs ) {
cout << "Number of processes must be a perfect square\n";
shutdown=true;
}
else {
nsamps=stoi(argv[1]);
}
}
MPI_Bcast(&shutdown,1,MPI_CXX_BOOL,0,MPI_COMM_WORLD);
if (shutdown) {
MPI_Finalize();
exit(1);
}
MPI_Bcast(&nsamps,1,MPI_INT,0,MPI_COMM_WORLD);
// Define the parameters to test
float pi=4.0*atan(1.0);
float xlo=-10.*pi;
float xhi=10.*pi;
float ylo=-10.*pi;
float yhi=10.*pi;
float x_subrange=(xhi-xlo)/ncols;
float y_subrange=(yhi-ylo)/nrows;
// Calculate the range over which I will be working
int col_num=rank%ncols;
int row_num=rank/nrows;
float my_xlo=xlo+col_num*x_subrange;
float my_xhi=my_xlo+x_subrange;
float my_ylo=ylo+row_num*y_subrange;
float my_yhi=my_ylo+y_subrange;
srand(time(0)+rank);
float xmax=0.;
float ymax=0.;
float zmax=0.;
for (int i=0;i<nsamps;++i) {
for (int j=0;j<nsamps;++j) {
xval=my_xlo+(my_xhi-my_xlo)*urand;
yval=my_ylo+(my_yhi-my_ylo)*urand;
zval=surface(xval,yval);
if (zval>zmax) {
zmax=zval;
xmax=xval;
ymax=yval;
}
}
}
float *xresult=new float[nprocs];
float *yresult=new float[nprocs];
float *zresult=new float[nprocs];
MPI_Gather(&xmax,1,MPI_FLOAT,xresult,1,MPI_FLOAT,0,MPI_COMM_WORLD);
MPI_Gather(&ymax,1,MPI_FLOAT,yresult,1,MPI_FLOAT,0,MPI_COMM_WORLD);
MPI_Gather(&zmax,1,MPI_FLOAT,zresult,1,MPI_FLOAT,0,MPI_COMM_WORLD);
if (rank==0) {
float g_zmax=zresult[0];
float g_xmax=xresult[0];
float g_ymax=yresult[0];
for (int i=1;i<nprocs;++i) {
if (zresult[i] > g_zmax) {
g_zmax=zresult[i];
g_xmax=xresult[i];
g_ymax=yresult[i];
}
}
cout<<"Result is "<<g_zmax<<" at x,y="<<g_xmax<<", "<<g_ymax<<endl;
}
MPI_Finalize();
}
Fortran
module random
implicit none
! Author: Katherine Holcomb
! Shortened version of a longer module
! Module incorporated into this file for convenience; typically it would be in its
! own file.
! Comment out one or the other when the module is incorporated into a code.
! Single precision
integer, parameter :: rk = kind(1.0)
! Double precision
!integer, parameter :: rk = kind(1.0d0)
contains
subroutine set_random_seed(seed)
! Sets all elements of the seed array
integer, optional, intent(in) :: seed
integer :: isize
integer, dimension(:), allocatable :: iseed
integer, dimension(8) :: idate
integer :: icount, i
call random_seed(size=isize)
if ( .not. present(seed) ) then
call system_clock(icount)
allocate(iseed(isize),source=icount+370*[(i,i=0,isize-1)])
else
allocate(iseed(isize))
iseed=seed
endif
call random_seed(put=iseed)
end subroutine set_random_seed
function urand(lb,ub,seed)
! Returns a uniformly-distributed random number in the range lb to ub.
real(rk) :: urand
real(rk), optional, intent(in) :: lb,ub
real(rk), optional, intent(in) :: seed
integer :: iseed
real(rk) :: rnd
real(rk) :: lower,upper
if ( present(seed) ) then
iseed=int(seed)
call set_random_seed(iseed)
endif
if ( present(lb) ) then
lower=lb
else
lower=0.0_rk
endif
if ( present(ub) ) then
upper = ub
else
upper = 1.0_rk
endif
call random_number(rnd)
urand = lower+(upper-lower)*rnd
return
end function urand
end module
program find_max
use random
use mpi
implicit none
real :: pi=4.0*atan(1.0)
real :: xlo, xhi, ylo, yhi
real :: zval, zmax
real :: xval, xincr, xmax
real :: yval, yincr, ymax
real, dimension(:), allocatable :: xvals, yvals
real, dimension(:,:), allocatable :: zvals
integer :: i, j, nargs
integer :: nsamps
character(len=12) :: n
integer :: rank, nprocs, ierr
integer, dimension(:), allocatable:: seed
integer :: iseed, icount
integer, dimension(:), allocatable:: maxinds
real, dimension(:), allocatable:: xresult,yresult,zresult
real :: g_zmax
real :: rows
real :: x_subrange,y_subrange
real :: my_xlo,my_xhi,my_ylo,my_yhi
integer :: nrows,ncols
integer :: row_num, col_num
logical :: shutdown=.false.
interface
real function surface(x,y)
implicit none
real, intent(in) :: x, y
end function
end interface
call MPI_Init(ierr)
call MPI_Comm_rank(MPI_COMM_WORLD,rank,ierr)
call MPI_Comm_size(MPI_COMM_WORLD,nprocs,ierr)
! For this example we'll use perfect square nprocs. Otherwise we have to
! tell it how to divide up the processes into rows and columns.
rows=sqrt(real(nprocs))
nrows=int(rows)
ncols=nrows
if (rank==0) then
nargs=command_argument_count()
if ( nargs .ne. 1 ) then
shutdown=.true.
write(*,*) "Usage: number of samples to test"
else if ( int(rows+0.5)**2 /= nprocs ) then
write(*,*) "Number of processes must be a perfect square"
shutdown=.true.
else
call get_command_argument(1,n)
read(n,'(i12)') nsamps
endif
endif
call MPI_Bcast(shutdown,1,MPI_LOGICAL,0,MPI_COMM_WORLD,ierr)
if (shutdown) then
call MPI_Finalize(ierr)
stop
endif
call MPI_Bcast(nsamps,1,MPI_INTEGER,0,MPI_COMM_WORLD,ierr)
! Define the parameters to test
xlo=-10.*pi; xhi=10.*pi
ylo=-10.*pi; yhi=10.*pi
x_subrange=(xhi-xlo)/ncols
y_subrange=(yhi-ylo)/nrows
! Calculate the range over which I will be working
my_xlo=xlo+col_num*x_subrange;
my_xhi=my_xlo+x_subrange;
my_ylo=ylo+row_num*y_subrange;
my_yhi=my_ylo+y_subrange;
!For correct statistical properties, we set random seeds for each rank
call system_clock(icount)
iseed=icount+rank
call set_random_seed(iseed)
xmax=0.
ymax=0.
zmax=0.
do i=1,nsamps
do j=1,nsamps
xval=urand(xlo,xhi)
yval=urand(ylo,yhi)
zval=surface(xval,yval)
if (zval>zmax) then
zmax=zval
xmax=xval
ymax=yval
endif
enddo
enddo
! If not allgather, only root needs to allocate
if (rank==0) then
allocate(maxinds(nprocs))
allocate(xresult(nprocs),yresult(nprocs),zresult(nprocs))
endif
call MPI_Gather(xmax,1,MPI_REAL,xresult,1,MPI_REAL,0,MPI_COMM_WORLD,ierr)
call MPI_Gather(ymax,1,MPI_REAL,yresult,1,MPI_REAL,0,MPI_COMM_WORLD,ierr)
call MPI_Gather(zmax,1,MPI_REAL,zresult,1,MPI_REAL,0,MPI_COMM_WORLD,ierr)
if (rank==0) then
g_zmax=maxval(zresult)
maxinds=maxloc(zresult)
write(*,'(a,f0.6,a,f0.6,a,f0.6)') &
"Result is ",g_zmax," at x,y=",xresult(maxinds(1)),", ",yresult(maxinds(1))
endif
call MPI_Finalize(ierr)
end program
real function surface(x,y)
implicit none
real, intent(in) :: x, y
real :: pi=4.0*atan(1.0)
real :: mu1, mu2, sig1, sig2
real :: a, b
real :: z1, z2
mu1=sqrt(2.0)
mu2=sqrt(pi)
sig1=3.1
sig2=1.4
z1=0.1*sin(x)*sin(x*y)
a=(x-mu1)**2/(2*sig1**2)
b=(y-mu2)**2/(2*sig2**2)
z2=exp(-(a+b))/(sig1*sig2*sqrt(2.0*pi))
surface=z1+z2
end function
Python
from mpi4py import MPI
import numpy as np
import sys
def surface(x,y):
"""This is the main processing function. We use a ufunc for MPI."""
mu1=np.sqrt(2.0)
mu2=np.sqrt(np.pi)
sig1=3.1
sig2=1.4
z1=0.1*np.sin(x)*np.sin(x*y)
a=(x-mu1)**2/(2*sig1**2)
b=(y-mu2)**2/(2*sig2**2)
z2=np.exp(-(a+b))/(sig1*sig2*np.sqrt(2.0*np.pi))
z=z1+z2
return z
if __name__ == '__main__':
comm=MPI.COMM_WORLD
rank=comm.Get_rank()
nprocs=comm.Get_size()
shutdown=None
nsamps=0
# For this example we'll use perfect square nprocs. Otherwise we have
# to tell it how to divide up the processes into rows and columns.
nrows=np.sqrt(nprocs)
ncols=nrows
if rank==0:
if int(ncols+0.5)**2 != nprocs:
print("Number of processes must be a perfect square")
shutdown=True
elif len(sys.argv)==2:
nsamps=int(float(sys.argv[1]))
shutdown=False
else:
print("Usage: number of samples")
shutdown=True
shutdown=comm.bcast(shutdown,root=0)
if shutdown:
MPI.Finalize()
nsamps=comm.bcast(nsamps,root=0)
#Fairly crude effort to get different seeds on different processes
rng = np.random.default_rng()
# Define the parameters to test
xlo=-10.*np.pi; xhi=10.*np.pi
ylo=-10.*np.pi; yhi=10.*np.pi
x_subrange=(xhi-xlo)/ncols
y_subrange=(yhi-ylo)/nrows
# Calculate the range over which I will be working
col_num=rank%ncols
row_num=rank//nrows
my_xlo=xlo+col_num*x_subrange
my_xhi=my_xlo+x_subrange
my_ylo=ylo+row_num*y_subrange
my_yhi=my_ylo+y_subrange
tic=MPI.Wtime()
#We would usually have a lot of x,y points so cannot create z as a function
#of x and y, so have to use a loop
zmax=0.
for i in range(nsamps):
for j in range(nsamps):
xval=rng.uniform(my_xlo,my_xhi)
yval=rng.uniform(my_ylo,my_yhi)
zval=surface(xval,yval)
if zval>zmax:
zmax=zval
xmax=xval
ymax=yval
max_xind=i
max_yind=j
my_xresult=np.array([xmax])
my_yresult=np.array([ymax])
my_zresult=np.array([zmax])
xresult=np.empty(nprocs)
yresult=np.empty(nprocs)
zresult=np.empty(nprocs)
comm.Gather([my_xresult,MPI.FLOAT],[xresult,MPI.FLOAT])
comm.Gather([my_yresult,MPI.FLOAT],[yresult,MPI.FLOAT])
comm.Gather([my_zresult,MPI.FLOAT],[zresult,MPI.FLOAT])
toc=MPI.Wtime()
if rank==0:
g_zmax=zresult.max()
maxind=np.argmax(zresult)
g_xmax=xresult[maxind]
g_ymax=yresult[maxind]
print(f"Result is {g_zmax:.4f} at x,y= {g_xmax:.4f},{g_ymax:.4f} ")
MPI.Finalize()