Jacobi Iteration

There are many algorithms for solving the Laplace equation, but we will use one of the oldest, the Jacobi method. It is typically slow to converge to the solution, but it is easy to understand, easy to program, and easy to parallelize.

This method uses two arrays. Omitting the derivation, given the current values of array $u$ we compute the new value with the equation

w[i,j] = u[i-1,j] + u[i+1,j] + u[i,j-1] + u[i,j+1])

You may notice that the “updated” value at a given point is just the average of its neighbors. Boundary values must be provided for appropriate values of $i$ and $j$; in our previous study of halos, we used $i=0$, $i=nr+1$, $j=0$, and $j=nc+1$ for the boundary values, with the solution defined for $i=1..nr$, $j=1..nc$.

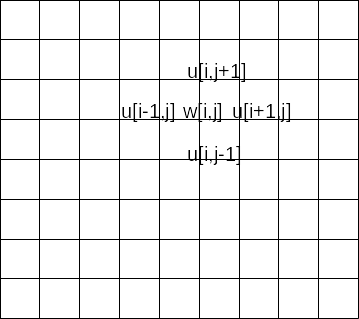
Before we begin, we must determine the tolerance $\epsilon$ for an acceptable solution. We make a sweep through the grid, computing the new values $w$ at each grid point. We compare all these values to the old value at the same point. If

$$ | w - u | < \epsilon $$

for all $w_{ij}$, we terminate the iterations. Otherwise we set $u=w$ at all interior points and make another sweep through the grid.

In a Python-like pseudocode the algorithm is

#Set a very large maximum number of iterations


#Set boundary conditions
u[0,:]=topBC
u[nr+1,:]=bottomBC
u[:,0]=leftBC
u[:,nc+1]=rightBC

#Make an initial guess for the solution. Zero is often reasonable.
u[1:nr,1:nc]=0.  

#Set tolerance
eps=1.e-8

#Loop over a maximum number of iterations
do while (iter<maxiter)
   do i=1,nr
      do j=1,nc
         w[i,j]=0.25*(u[i-1,j] + u[i+1,j] + u[i,j-1] + u[i,j+1])
      end
   end
   #Remember to compare only inner values
   if maximum(abs(w[1:nr,1:nc]-u[1:nr,1:nc]))<eps then
      break #exit iteration loop
   else
      u[1:nr,1:nc]=w[1:nr,1:nc]
   end
   #reapply boundary conditions if appropriate, should not be needed here
   #u[0,:]=topBC etc.
   
end

#Output result to a file

This method sets a maximum number of iterations, to prevent an effectively infinite loop in case the method doesn’t converge, which it should do in nearly all cases; we then break out of the loop once convergence is achieved. Alternatively we could loop until convergence is achieved; in this case we would need to set u and w differently at the beginning and it would be prudent to keep a count of the number of iterations and check whether the maximum was exceeded.