Timing and Benchmarking
We should always benchmark our parallel programs to make sure we are utilizing resources effectively, especially if we are running on multi-user systems that may require justifications, proposals, or charges for time. MPI provides procedures to time all or portions of a program that can be used regardless of how many processes are invoked. These routines are portable and are the same for all languages that support MPI.
Wtime and Wtick
MPI_Wtime returns a double-precision floating-point number representing the time in seconds that has elapsed since some particular time in the past. To time parts of the execution, a starting time and an ending time must be specified and the difference obtained.
Since MPI processes run independently, it does not make sense to compare a start time on one process with an end time on another process. Only differences on the same process are significant. For an overall time we can often use rank 0.
MPI_Wtick returns the resolution, in seconds, for each “tick” of the timer. This may be of interest for profiling.
The syntax of both procedures is very simple.
C++
double startTime=MPI_Wtime();
double tick=MPI_Wtick();
Fortran
Unlike most MPI routines, Wtime and Wtick are functions in Fortran.
double precision :: start_time, tick
start_time=MPI_Wtime()
tick=MPI_Wtick()
Python
start_time=MPI.Wtime()
tick=MPI_Wtick()
Scaling and Efficiency Studies
In a previous chapter we learned about scaling and efficiency. Let us apply this to our random_walk program.
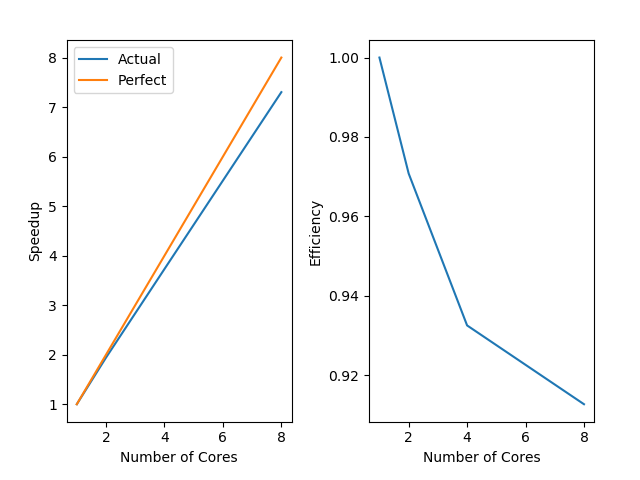
Copy the code from that chapter in your language of choice for this exercise. Add appropriate timing procedures. It is only necessary to print the result from rank 0. Run the timed random-walk code over 1, 2, 4, and 8 processes for some number of “steps” that will run at least several seconds. Use any plotting package you know to plot speedup versus number of processes/cores. Add a curve for perfect speedup. Plot the parallel efficiency versus core number. (Recall that the theoretical maximum efficiency is 1.)
The random-walk program is “embarrassingly parallel” since there is as yet no communication among processes. We did not have to use MPI but could have run multiple tests and collected the results. There is some small overhead in using MPI.
C++
/* Solves a random-walk problem by a brute-force method.
*
*/
#include <iostream>
#include <string>
#include <sstream>
#include <random>
#include <cmath>
#include <mpi.h>
using namespace std;
int main(int argc, char **argv) {
random_device rd;
mt19937 rng(rd());
uniform_int_distribution<int> choice(1,4);
int npes, rank;
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &npes);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
long long N;
if (argc != 2) {
cout<<rank<<":0,0,0\n";
MPI_Finalize();
return 0;
}
else {
string steps=argv[1];
stringstream ssteps;
ssteps<<steps;
ssteps>>N;
}
//Start timing after reading the arguments
double startTime=MPI_Wtime();
double x=0.;
double y=0.;
int direction;
for (long long i=1; i<=N; ++i) {
direction=choice(rng);
switch (direction) {
case 1:
x+=1.;
break;
case 2:
x-=1.;
break;
case 3:
y+=1.;
break;
case 4:
y-=1.;
break;
}
}
double eucDist=sqrt(x*x+y*y);
cout<<rank<<":"<<N<<","<<sqrt((double)N)<<","<<eucDist<<"\n";
//Stop timing
if (rank==0) {
cout<<"The timer resolution is "<<MPI_Wtick()<<endl;
cout<<"Time to solution "<<MPI_Wtime()-startTime<<endl;
}
MPI_Finalize();
return 0;
}
Fortran
module random
implicit none
! Author: Katherine Holcomb
! Shortened version of a longer module
! Module incorporated into this file for convenience; typically it would be in its
! own file.
! Comment out one or the other when the module is incorporated into a code.
! Single precision
!integer, parameter :: rk = kind(1.0)
! Double precision
integer, parameter :: rk = kind(1.0d0)
contains
subroutine set_random_seed(seed)
! Sets all elements of the seed array
integer, optional, intent(in) :: seed
integer :: isize
integer, dimension(:), allocatable :: iseed
integer, dimension(8) :: idate
integer :: icount, i
call random_seed(size=isize)
if ( .not. present(seed) ) then
call system_clock(icount)
allocate(iseed(isize),source=icount+370*[(i,i=0,isize-1)])
else
allocate(iseed(isize))
iseed=seed
endif
call random_seed(put=iseed)
end subroutine set_random_seed
function urand(lb,ub,seed)
! Returns a uniformly-distributed random number in the range lb to ub.
real(rk) :: urand
real(rk), optional, intent(in) :: lb,ub
real(rk), optional, intent(in) :: seed
integer :: iseed
real(rk) :: rnd
real(rk) :: lower,upper
if ( present(seed) ) then
iseed=int(seed)
call set_random_seed(iseed)
endif
if ( present(lb) ) then
lower=lb
else
lower=0.0_rk
endif
if ( present(ub) ) then
upper = ub
else
upper = 1.0_rk
endif
call random_number(rnd)
urand = lower+(upper-lower)*rnd
return
end function urand
function randint(n,m)
! Returns a random integer between n and m.
integer :: randint
integer, intent(in) :: n,m
randint=ceiling(urand(real(n-1,rk),real(m,rk)))
end function randint
end module random
program random_walk
use random
use mpi
implicit none
integer, parameter :: ik = selected_int_kind(15)
integer :: nargs
character(len=10) :: ns,nexp
integer :: m, step
real, dimension(2) :: pos, move
real :: distance
double precision :: start_time
integer :: rank, npes, ierr
integer(ik) :: n, nsteps
call MPI_Init(ierr)
call MPI_Comm_size(MPI_COMM_WORLD,npes,ierr)
call MPI_Comm_rank(MPI_COMM_WORLD,rank,ierr)
nargs=command_argument_count()
if ( nargs .ne. 1 ) then
write(*,*) rank,":", 0, 0., 0.
call MPI_Finalize(ierr)
stop
else
call get_command_argument(1,ns)
read(ns,'(i10)') nsteps
endif
call set_random_seed()
!Start timing after reading arguments
start_time=MPI_Wtime()
pos=[0.,0.]
do n=1,nsteps
step=randint(1,4)
if (step==1) then
move=[0.,1.]
else if (step==2) then
move=[0.,-1.]
else if (step==3) then
move=[1.,0.]
else
move=[-1.,0.]
endif
pos=pos+move
enddo
distance=sqrt(pos(1)**2+pos(2)**2)
write(*,*) rank,":",nsteps, sqrt(real(nsteps)), distance
!End timing
if (rank==0) then
print *, "The timer resolution is ",MPI_Wtick()
print *, "Time to solution ",MPI_Wtime()-start_time
endif
call MPI_Finalize(ierr)
end program
Python
import numpy as np
import random
import sys
import numpy as np
from mpi4py import MPI
comm=MPI.COMM_WORLD
myrank=comm.Get_rank()
nprocs=comm.Get_size()
if len(sys.argv)>1:
Nsteps=int(sys.argv[1])
else:
print(0, 0., 0.)
sys.exit()
# Start timing after reading arguments
start_time=MPI.Wtime()
pos=np.array([0,0])
moves=[np.array([0,1]),np.array([0,-1]),np.array([1,0]),np.array([-1,0])]
for n in range(Nsteps):
move=random.choice(moves)
pos+=move
distance=np.sqrt(pos[0]**2+pos[1]**2)
print(Nsteps, np.sqrt(Nsteps), distance)
# End timing
if myrank==0:
print("The timer resolution is ",MPI.Wtick())
print("Time to solution ",MPI.Wtime()-start_time)
MPI.Finalize()
Strong Scaling
In strong scaling, a fixed amount of work is distributed over a varying number of processes. The timed random-walk code is written to implement weak scaling; the number of steps provided is the number each process will compute, so we must adjust the number of steps to keep the amount of work constant over different numbers of processes. The example solution used the Python version with $10^{7}$ steps for the serial code. That was then divided by 2, 4, and 8 for subsequent runs.
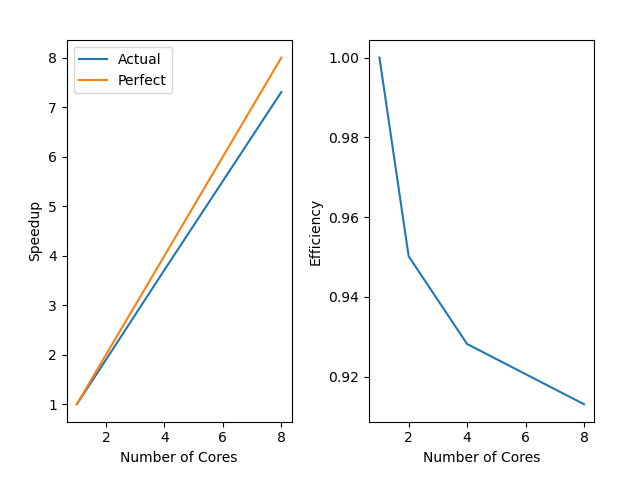
Weak Scaling
Recall that weak scaling increases the amount of work as the process number increases. Ideally, the quantity of work per process is the same across all proceses. For weak scaling, we must compute the serial time for the equivalent sized problem, so the serial code must be run for $8 \times 10^{7}$, $4 \times 10^{7}$, and $2 \times 10^{7}$ as well as for $10^{7}$ steps. Plot the scaling compared to perfect scaling of $p$. Compute and plot the parallel efficiency for these runs. Was it similar to strong scaling? Why might this be the case for this particular example?