MPI Project Set 1
Project 1
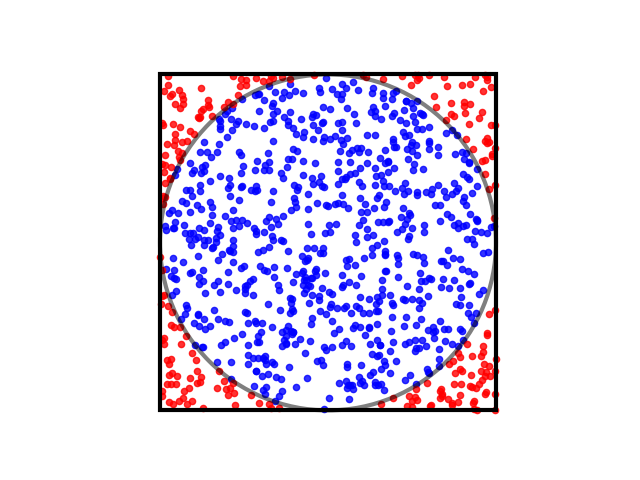
A very inefficient way to compute $\pi$ is to use a Monte Carlo method. In this we randomly throw “darts” at a circle of radius 1 within a square with sides of length 2. The ratio of the areas is thus $\pi \div 4$. If we compute the ratio of “hits” that land within the circle to the total number of throws, then our estimate of $\pi$ is $4 \times \mathrm{ratio}$.
Write a program that computes pi by this method. Start with a serial code and test it for a relatively small number of “dart throws.” You will find it very inaccurate for a small number of throws but should be able to obtain an estimate at least close to 3. Once you are satisfied that your program works in serial, parallelize it. Distribute the throws over N processes and use a reduction to get the totals for your overall estimate of pi. Test your parallel code with 8 processes and 1e9 throws. Hint: C++ programmers should use long long for the number of throws and any corresponding loop counter. Fortran programmers should use an 8-byte integer. (See the C++ and Fortran random-walk examples.) Python automatically handles large integers.
Note that the formula is the same if one considers only the upper right quadrant of the figure.
Fortran programmers: you may wish to extract the random module from mpirandomwalk.f90 into a separate file random.f90, since it is used frequently. Remember that modules must be compiled before any program units that USE them.
Try to write the serial code before peeking at the examples.
Serial Codes
C++
/* Computes pi by a Monte-Carlo method
*
*/
#include <iostream>
#include <iomanip>
#include <string>
#include <sstream>
#include <random>
#include <cmath>
using namespace std;
#define urand ((double)rand()/(double)RAND_MAX);
long long throwDarts(long long nThrows) {
long long hits=0;
for (int i=0; i<nThrows; ++i) {
double x = urand;
double y = urand;
if ( sqrt(pow(x,2)+pow(y,2)) < 1.0 ) {
hits++;
}
}
return hits;
}
int main(int argc, char **argv) {
long long nThrows;
if (argc != 2) {
cout<<"Usage: nThrows\n";
return 0;
}
else {
string steps=argv[1];
stringstream ssteps;
ssteps<<steps;
ssteps>>nThrows;
}
//It's better to use C++ random-number generators, but that requires some
//additional coding, and possibly templating, so let's keep it simple and
//fast for this example.
srand(time(0));
long long nHits=throwDarts(nThrows);
double pi=4.0*(double)nHits/(double)nThrows;
cout<<"Pi is "<<setprecision(6)<<pi<<endl;
return 0;
}
Fortran
!*******************************************************************************
! Program to compute pi using a Monte-Carlo integration
!
! Author: K. Holcomb
! Date : 20180424
!
!*******************************************************************************
module random
implicit none
! Author: Katherine Holcomb
! Shortened version of a longer module
! Module incorporated into this file for convenience; typically it would be in its
! own file.
! Comment out one or the other when the module is incorporated into a code.
! Single precision
!integer, parameter :: rk = kind(1.0)
! Double precision
integer, parameter :: rk = kind(1.0d0)
contains
subroutine set_random_seed(seed)
! Sets all elements of the seed array
integer, optional, intent(in) :: seed
integer :: isize
integer, dimension(:), allocatable :: iseed
integer, dimension(8) :: idate
integer :: icount, i
call random_seed(size=isize)
if ( .not. present(seed) ) then
call system_clock(icount)
allocate(iseed(isize),source=icount+370*[(i,i=0,isize-1)])
else
allocate(iseed(isize))
iseed=seed
endif
call random_seed(put=iseed)
end subroutine set_random_seed
function urand(lb,ub,seed)
! Returns a uniformly-distributed random number in the range lb to ub.
real(rk) :: urand
real(rk), optional, intent(in) :: lb,ub
real(rk), optional, intent(in) :: seed
integer :: iseed
real(rk) :: rnd
real(rk) :: lower,upper
if ( present(seed) ) then
iseed=int(seed)
call set_random_seed(iseed)
endif
if ( present(lb) ) then
lower=lb
else
lower=0.0_rk
endif
if ( present(ub) ) then
upper = ub
else
upper = 1.0_rk
endif
call random_number(rnd)
urand = lower+(upper-lower)*rnd
return
end function urand
end module
program piMC
use random
implicit none
integer, parameter :: ik = selected_int_kind(15)
character(len=12) :: throws
integer :: nargs
integer(ik) :: n_throws, n_hits
double precision :: pi
integer(ik) :: n
interface
function throw_darts(n_throws)
integer, parameter :: ik = selected_int_kind(15)
integer(ik) :: throw_darts
integer(ik), intent(in) :: n_throws
end function throw_darts
end interface
nargs=command_argument_count()
if (nargs .lt. 1) then
n_throws=1000000000 ! default
else
call get_command_argument(1,throws)
read(throws,'(i12)') n_throws
endif
call set_random_seed()
n_hits=throw_darts(n_throws)
pi=4.0d0*dble(n_hits)/dble(n_throws)
write(*,'(f12.8)') pi
end program piMC
function throw_darts(n_throws)
use random
integer, parameter :: ik = selected_int_kind(15)
integer(ik) :: throw_darts
integer(ik), intent(in) :: n_throws
integer(ik) :: i,hits
double precision :: x, y
hits=0
do i=1,n_throws
x=urand(0.d0,1.d0)
y=urand(0.d0,1.d0)
if (sqrt(x**2+y**2)<1.0) then
hits=hits+1
endif
enddo
throw_darts=hits
end function throw_darts
Python
"""
This program estimates the value of PI by running a Monte Carlo simulation.
NOTE: This is not how one would normally want to calculate PI, but serves
to illustrate the principle.
"""
import sys
import os
import math
import numpy as np
def throw(numPoints):
"""Throw a series of imaginary darts at an imaginary dartboard of unit
radius and count how many land inside the circle."""
x=np.random.random(numPoints)
y=np.random.random(numPoints)
inside=(x**2+y**2)<=1.0
numInside=sum(inside)
return numInside
def main():
if (len(sys.argv)>1):
try:
numPoints=int(float((sys.argv[1])))
except:
print("Argument must be an integer.")
else:
print("USAGE:python MonteCarlo.py numPoints")
exit()
numInside=throw(numPoints)
ppi=4.*numInside/float(numPoints)
print(ppi)
if __name__=="__main__":
main()
Example Solutions
C++
/* Computes pi by a Monte-Carlo method
*
*/
#include <iostream>
#include <iomanip>
#include <string>
#include <sstream>
#include <random>
#include <cmath>
#include <mpi.h>
using namespace std;
#define urand ((double)rand()/(double)RAND_MAX);
long long throwDarts(long long nThrows) {
long long hits=0;
for (int i=0; i<nThrows; ++i) {
double x = urand;
double y = urand;
if ( sqrt(pow(x,2)+pow(y,2)) < 1.0 ) {
hits++;
}
}
return hits;
}
int main(int argc, char **argv) {
int nprocs, rank;
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
long long nThrows;
if (argc != 2) {
cout<<rank<<"Usage: nThrows\n";
MPI_Finalize();
return 0;
}
else {
string steps=argv[1];
stringstream ssteps;
ssteps<<steps;
ssteps>>nThrows;
}
//It's better to use C++ random-number generators, but that requires some
//additional coding, and possibly templating, so let's keep it simple and
//fast for this example.
srand(time(0));
// Strong scaling
long long myThrows=nThrows/nprocs;
if ( nThrows%nprocs!=0 ) {
long long nExtra=nThrows%nprocs; // dopey load balancing
for (long long n=1;n<=nExtra;n++) {
if (n-1==rank) myThrows++;
}
}
// For weak scaling
// myThrows=nThrows
//
long long myHits=throwDarts(myThrows);
long long allHits;
MPI_Reduce(&myHits,&allHits,1,MPI_LONG_LONG_INT,MPI_SUM,0,MPI_COMM_WORLD);
double pi=4.*(double)allHits/(double)myThrows;
//weak scaling
// double pi=(double)allHits/(double)myThrows*nprocs;
if (rank==0) {
cout<<"Pi is "<<setprecision(6)<<pi<<endl;
}
MPI_Finalize();
return 0;
}
Fortran
!*******************************************************************************
! Program to compute pi using a Monte-Carlo integration
!
! Author: K. Holcomb
! Date : 20180424
!
!*******************************************************************************
module random
implicit none
! Author: Katherine Holcomb
! Shortened version of a longer module
! Module incorporated into this file for convenience; typically it would be in its
! own file.
! Comment out one or the other when the module is incorporated into a code.
! Single precision
!integer, parameter :: rk = kind(1.0)
! Double precision
integer, parameter :: rk = kind(1.0d0)
contains
subroutine set_random_seed(seed)
! Sets all elements of the seed array
integer, optional, intent(in) :: seed
integer :: isize
integer, dimension(:), allocatable :: iseed
integer, dimension(8) :: idate
integer :: icount, i
call random_seed(size=isize)
if ( .not. present(seed) ) then
call system_clock(icount)
allocate(iseed(isize),source=icount+370*[(i,i=0,isize-1)])
else
allocate(iseed(isize))
iseed=seed
endif
call random_seed(put=iseed)
end subroutine set_random_seed
function urand(lb,ub,seed)
! Returns a uniformly-distributed random number in the range lb to ub.
real(rk) :: urand
real(rk), optional, intent(in) :: lb,ub
real(rk), optional, intent(in) :: seed
integer :: iseed
real(rk) :: rnd
real(rk) :: lower,upper
if ( present(seed) ) then
iseed=int(seed)
call set_random_seed(iseed)
endif
if ( present(lb) ) then
lower=lb
else
lower=0.0_rk
endif
if ( present(ub) ) then
upper = ub
else
upper = 1.0_rk
endif
call random_number(rnd)
urand = lower+(upper-lower)*rnd
return
end function urand
end module
program piMC
use mpi
use random
implicit none
integer, parameter :: ik = selected_int_kind(15)
character(len=12) :: throws
integer :: nargs
integer(ik) :: my_nthrows, my_hits, n_extra, n_throws, n_hits
double precision :: pi
integer :: rank, nprocs, ierr
integer(ik) :: n
interface
function throw_darts(n_throws)
integer, parameter :: ik = selected_int_kind(15)
integer(ik) :: throw_darts
integer(ik), intent(in) :: n_throws
end function throw_darts
end interface
nargs=command_argument_count()
if (nargs .lt. 1) then
n_throws=1000000000 ! default, if not wanted then stop
else
call get_command_argument(1,throws)
read(throws,'(i12)') n_throws
endif
call MPI_Init(ierr)
call MPI_Comm_size(MPI_COMM_WORLD,nprocs,ierr)
call MPI_Comm_rank(MPI_COMM_WORLD,rank,ierr)
call set_random_seed()
! For strong scaling
my_nthrows=n_throws/nprocs
n_extra=mod(n_throws,nprocs) ! dopey load balancing
if ( n_extra /=0 ) then
do n=1,n_extra
if (n-1==rank) my_nthrows=my_nthrows+1
enddo
endif
! For weak scaling
! my_nthrows=n_throws
! change final denominator to npes*n_throws
my_hits=throw_darts(my_nthrows)
call MPI_Reduce(my_hits,n_hits,1,MPI_INTEGER8,MPI_SUM,0,MPI_COMM_WORLD,ierr)
pi=4.0d0*dble(n_hits)/dble(n_throws)
if ( rank==0 ) then
write(*,'(f12.8)') pi
endif
!weak scaling
! pi=4.0d0*dble(n_hits)/dble(nprocs*n_throws)
call MPI_Finalize(ierr)
end program piMC
function throw_darts(n_throws)
use random
integer, parameter :: ik = selected_int_kind(15)
integer(ik) :: throw_darts
integer(ik), intent(in) :: n_throws
integer(ik) :: i,hits
double precision :: x, y
hits=0
do i=1,n_throws
x=urand(0.d0,1.d0)
y=urand(0.d0,1.d0)
if (sqrt(x**2+y**2)<1.0) then
hits=hits+1
endif
enddo
throw_darts=hits
end function throw_darts
Python
"""
This program estimates the value of PI by running a Monte Carlo simulation.
NOTE: This is not how one would normally want to calculate PI, but serves
to illustrate the principle.
"""
import sys
import os
import math
import numpy as np
from mpi4py import MPI
def throw(numPoints):
"""Throw a series of imaginary darts at an imaginary dartboard of unit
radius and count how many land inside the circle."""
x=np.random.random(numPoints)
y=np.random.random(numPoints)
inside=(x**2+y**2)<=1.0
numInside=sum(inside)
return numInside
def main():
if (len(sys.argv)>1):
try:
numPoints=int(float((sys.argv[1])))
except:
print("Argument must be an integer.")
else:
print("USAGE:python MonteCarlo.py numPoints")
exit()
myrank = MPI.COMM_WORLD.Get_rank()
nprocs = MPI.COMM_WORLD.Get_size()
#Distribute points
#Simple-minded method to distribute equally if the division isn't even.
chunks=numPoints%nprocs
myNumPoints=[numPoints//nprocs+1]*chunks+[numPoints//nprocs]*(nprocs-chunks)
tic=MPI.Wtime()
myInside=np.ones(1)*throw(myNumPoints[myrank])
allInside=np.zeros(1)
MPI.COMM_WORLD.Reduce(myInside, allInside, op=MPI.SUM, root=0)
ppi=4.*allInside/float(numPoints)
toc=MPI.Wtime()
if myrank==0:
print(ppi[0])
print("Time on "+str(nprocs)+" cores:"+str(round(toc-tic,4)))
if __name__=="__main__":
main()
Project 2
The trapezoid rule is a simple method for numerical quadrature (integration). Given a function $f(x)$, the integral from $x=a$ to $x=b$ is $$ I = \int^b_a f(x)dx $$ We can approximate the area under the curve as a trapezoid with area $$ I_{trap} = \frac{1}{2}(b-a)(f(b)+f(a) $$ However, a single trapezoid isn’t a very good approximation. We can improve our result by dividing the area under the curve into many trapezoids: $$ I_{trap} = \sum^n_{i=1} \frac{f(x_{i+1})+f(x_i)}{2} \Delta x_i $$ where $$ \Delta x_i = x_{i+1}-x_i $$ The larger the number of trapezoids, the more accurate our approximation to the integral will be. Typically $\Delta x_i$ is a constant usually represented by $h$, but that is not a requirement.
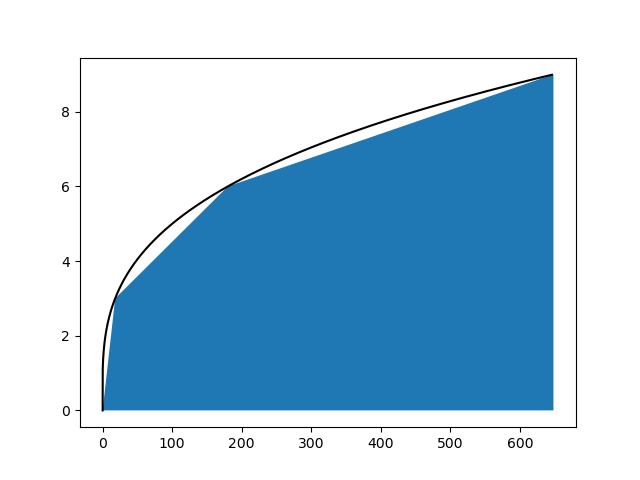
It should be clear that the trapezoid rule is very easy to parallelize. The interval on the independent variable should be split up among the ranks. Each rank then carries out the summation over its part. The complete integral is the sume of all ranks’ results.
Starting from the serial code in your language of choice, parallelize the trapezoid rule. Only rank 0 should read the input data; then it should broadcast appropriately to the other processes. Test for four processes. Note that the integral of the sine from 0 to $\pi$ has an exact value of 2, making it a good test case.
C++ and Fortran programmers: if you are not familiar with passing subprogram names as dummy variables, refer to our courses for Fortran or C++.
Serial Codes
C++
#include <iostream>
#include <iomanip>
#include <string>
#include <sstream>
#include <cmath>
//C++11
#include <functional>
using namespace std;
float f(float x) {
return sin(x);
}
//Function pointer
//float trap(float a, float b, float h, int n, float (*function)(float)) {
//Templated function object
float trap(float a, float b, float h, int n, function<float(float)> f) {
float integral = (f(a) + f(b))/2.0;
float x=a;
for (int i=0; i<n; ++i) {
x+=h;
integral += f(x);
}
integral *= h;
return integral;
}
int main(int argc, char **argv) {
// Calculate a definite integral using trapezoid rule
float a, b;
int n;
float h, integral;
float x;
if (argc != 4) {
cout<<"Usage: lower bound, upper bound, number of steps\n";
return 0;
}
else {
stringstream lb;
lb<<argv[1];
lb>>a;
a=stof(argv[1]);
stringstream ub;
ub<<argv[1];
ub>>b;
b=stof(argv[2]);
stringstream steps;
steps<<argv[3];
steps>>n;
}
h=(b-a)/n;
integral = trap(a,b,h,n,&f);
cout<<" Result "<<integral<<endl;
}
Fortran
program trapezoid
implicit none
! Calculate a definite integral using trapezoid rule
real :: a, b
integer :: n
real :: h, integral
real :: x
integer :: i, nargs
character(len=16) lb, ub, ns
interface
real function trap(f,a,b,h,n)
implicit none
real, intent(in) :: a, b, h
integer, intent(in) :: n
interface
real function f(x)
implicit none
real, intent(in) :: x
end function
end interface
end function
real function f(x)
implicit none
real, intent(in) :: x
end function
end interface
nargs=command_argument_count()
if ( nargs .ne. 3 ) then
stop "Usage: arguments are lower bound, upper bound, number of steps"
else
call get_command_argument(1,lb)
read(lb,'(f16.9)') a
call get_command_argument(2,ub)
read(ub,'(f16.9)') b
call get_command_argument(3,ns)
read(ns,'(i10)') n
endif
h=(b-a)/n
integral=trap(f,a,b,h,n)
print *, integral
end program
real function trap(f, a, b, h, n)
implicit none
real, intent(in) :: a, b, h
integer, intent(in) :: n
interface
real function f(x)
implicit none
real, intent(in) :: x
end function
end interface
real :: x
integer:: i
real :: integral
integral = (f(a) + f(b))/2.0
x=a
do i=1, n-1
x = x+h
integral = integral + f(x)
enddo
trap = integral*h
return
end function
real function f(x)
implicit none
real, intent(in):: x
f=sin(x)
end function
Python
import sys
import numpy as np
# Calculate a definite integral using trapezoid rule
# Does not use scipy so we can parallelize it
def f(x):
return np.sin(x)
def trap(a,b,h,n,f):
integral=(f(a) + f(b))/2.0
x=a
for i in range(n):
x+=h
integral+=f(x)
integral*=h
return integral
if len(sys.argv)==4:
a=float(sys.argv[1])
b=float(sys.argv[2])
n=int(float(sys.argv[3]))
else:
print("Usage: lower bound, upper bound, number of steps")
sys.exit()
h=(b-a)/n
integral=trap(a,b,h,n,f)
print("Result ",integral)
Example Solutions
C++
#include <iostream>
#include <iomanip>
#include <string>
#include <sstream>
#include <cmath>
//For templated function objects
#include <functional>
#include <mpi.h>
using namespace std;
float f(float x) {
return sin(x);
}
//Function pointer
//float trap(float a, float b, float h, int n, float (*function)(float)) {
//Templated function object
float trap(float a, float b, float h, int n, function<float(float)> f) {
float integral = (f(a) + f(b))/2.0;
float x=a;
for (int i=0; i<n; ++i) {
x+=h;
integral += f(x);
}
integral *= h;
return integral;
}
int main(int argc, char **argv) {
// Calculate a definite integral using trapezoid rule
float a, b;
int n;
float h, integral;
float x;
int nprocs, rank;
float total;
MPI_Init(&argc,&argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
bool shutdown=false;
if (rank==0) {
if (argc != 4) {
cout<<"Usage: lower bound, upper bound, number of steps\n";
shutdown=true;
}
else {
stringstream lb;
lb<<argv[1];
lb>>a;
a=stof(argv[1]);
stringstream ub;
ub<<argv[1];
ub>>b;
b=stof(argv[2]);
stringstream steps;
steps<<argv[3];
steps>>n;
}
//Not going to bother to redistribute this one
if (!shutdown) {
if (n%nprocs != 0) {
cout<<"Number of processes must evenly divide number of steps\n";
shutdown=true;
}
}
}
MPI_Bcast(&shutdown,1,MPI_CXX_BOOL,0,MPI_COMM_WORLD);
if (shutdown) {
MPI_Finalize();
exit(1);
}
MPI_Bcast(&a,1,MPI_REAL,0,MPI_COMM_WORLD);
MPI_Bcast(&b,1,MPI_REAL,0,MPI_COMM_WORLD);
MPI_Bcast(&n,1,MPI_INTEGER,0,MPI_COMM_WORLD);
h=(b-a)/n;
int local_n=n/nprocs;
float local_a=a+rank*local_n*h;
float local_b=b+rank*local_n*h;
integral = trap(local_a,local_b,h,local_n,&f);
MPI_Reduce(&integral,&total,1,MPI_FLOAT,MPI_SUM,0,MPI_COMM_WORLD);
if (rank==0) {
cout<<" Result "<<total<<endl;
}
}
Fortran
program trapezoid
use mpi
implicit none
! Calculate a definite integral using trapezoid rule
real :: a, b
integer :: n
real :: h, integral
real :: x
integer :: i, nargs
character(len=16) lb, ub, ns
real :: local_a, local_b, total
integer:: rank, nprocs, ierr, errcode
integer:: local_n
logical:: shutdown=.false.
interface
real function trap(f,a,b,h,n)
implicit none
real, intent(in) :: a, b, h
integer, intent(in) :: n
interface
real function f(x)
implicit none
real, intent(in) :: x
end function
end interface
end function
real function f(x)
implicit none
real, intent(in) :: x
end function
end interface
call MPI_Init(ierr)
call MPI_Comm_rank(MPI_COMM_WORLD, rank, ierr)
call MPI_Comm_size(MPI_COMM_WORLD, nprocs, ierr)
if (rank==0) then
nargs=command_argument_count()
if ( nargs .ne. 3 ) then
write(*,*) "Usage: arguments are lower bound, upper bound, number of steps"
shutdown=.true.
else
call get_command_argument(1,lb)
read(lb,'(f16.9)') a
call get_command_argument(2,ub)
read(ub,'(f16.9)') b
call get_command_argument(3,ns)
read(ns,'(i10)') n
shutdown=.false.
endif
if (.not. shutdown) then
!Don't bother to distribute number of steps, just stop if not even
if (mod(n,nprocs) /=0) then
write(*,*) "Number of processes must evenly divide number of steps"
shutdown=.true.
endif
endif
endif
call MPI_Bcast(shutdown,1,MPI_LOGICAL,0,MPI_COMM_WORLD,ierr)
if (shutdown) then
call MPI_Finalize(ierr)
stop
endif
call MPI_Bcast(a,1,MPI_REAL,0,MPI_COMM_WORLD,ierr)
call MPI_Bcast(b,1,MPI_REAL,0,MPI_COMM_WORLD,ierr)
call MPI_Bcast(n,1,MPI_INTEGER,0,MPI_COMM_WORLD,ierr)
h=(b-a)/n
local_n = n/nprocs
local_a = a + rank*local_n*h
local_b = local_a + local_n*h
integral = trap(f, local_a, local_b, h, local_n)
call MPI_Reduce(integral,total,1,MPI_REAL,MPI_SUM,0,MPI_COMM_WORLD,ierr)
if (rank .eq. 0) then
print *, total
endif
call MPI_Finalize(ierr)
end program
real function trap(f, a, b, h, n)
implicit none
real, intent(in) :: a, b, h
integer, intent(in) :: n
interface
real function f(x)
implicit none
real, intent(in) :: x
end function
end interface
real :: x
integer:: i
real :: integral
integral = (f(a) + f(b))/2.0
x=a
do i=1, n-1
x = x+h
integral = integral + f(x)
enddo
trap = integral*h
return
end function
real function f(x)
implicit none
real, intent(in):: x
f=sin(x)
end function
Python
import sys
import numpy as np
from mpi4py import MPI
# Calculate a definite integral using trapezoid rule
# Does not use scipy so we can parallelize it
def f(x):
return np.sin(x)
def trap(a,b,h,n,f):
integral=(f(a) + f(b))/2.0
x=a
for i in range(n):
x+=h
integral+=f(x)
integral*=h
return integral
def main():
comm=MPI.COMM_WORLD
nprocs=comm.Get_size()
rank=comm.Get_rank()
a=np.empty(1,dtype='float')
b=np.empty(1,dtype='float')
n=np.empty(1,dtype='int')
shutdown=None
if rank==0:
if len(sys.argv)==4:
a[0]=float(sys.argv[1])
b[0]=float(sys.argv[2])
n[0]=int(float(sys.argv[3]))
shutdown=False
else:
print("Usage: lower bound, upper bound, number of steps")
shutdown=True
#Not going to bother with redistributing on this one
if (not shutdown):
if n[0]%nprocs!=0:
print("The number of processes must evenly divide the number of steps ")
shutdown=True
#Note lower case and return value
shutdown=comm.bcast(shutdown,root=0)
if shutdown:
MPI.Finalize()
exit()
comm.Bcast([a,MPI.FLOAT],root=0)
comm.Bcast([b,MPI.FLOAT],root=0)
comm.Bcast([n,MPI.INT],root=0)
h=(b-a)/n
local_n=n[0]//nprocs
local_a=a[0]+rank*local_n*h
local_b=b[0]+rank*local_n*h
integral=np.empty(1,dtype='float')
integral[0]=trap(local_a,local_b,h,local_n,f)
total=np.empty(1)
comm.Reduce(integral,total,op=MPI.SUM)
if rank==0:
print("Result ",total)
MPI.Finalize()
if __name__=="__main__":
main()
Project 3
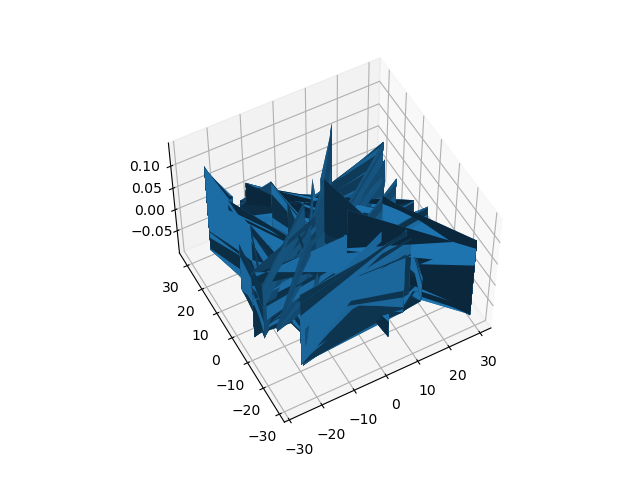
We wish to find the maximum of a 3-d surface described by a relatively complicated function. We can use a “brute force” method, which evaluates a large number of $x$ and $y$ values randomly distributed over the independent variables. This method of optimization is easily parallelized and can often be faster than older methods even when those are parallelized.
The surface is defined by the following rules:
$$ \mu_1 = \sqrt{2}\ ,\ \mu_2 = \sqrt{\pi}\ ,\ \sigma_1 = 3.1\ ,\ \sigma_2 = 1.4 $$ $$ z_1 = 0.1 \sin(x) \sin(y) $$ $$ a = \frac{(x - \mu_1)^2}{2\sigma_1^2}\ ,\ b = \frac{(y - \mu_2)^2}{2\sigma_2^2} $$ $$ z_2 = \frac{e^{(a+b)}}{\sigma_1 \sigma_2 \sqrt{2\pi}} $$ $$ z = z_1 + z_2 $$
We consider the ranges $$ -10\pi \le x \le 10\pi\ ,\ -10\pi \le y \le 10\pi $$
Generate a list of N random values for each of x and y over the above range. For testing you can use N=100000 for compiled languages and N=10000 for Python. Be sure to measure the time. Use appropriate MPI gathers to obtain not just the maximum value of $z$ from each process, but the corresponding $x$ and $y$ values. Remember that gather collects items in strict rank order. Use one or more built-ins for your language (maxloc for Fortran, np.argmax for Python) or loops (C/C++) to find the $x$, $y$, and $z$ for the maximum.
Serial Codes
C++
#include <iostream>
#include <iomanip>
#include <string>
#include <sstream>
#include <random>
#include <cmath>
using namespace std;
#define urand ((double)rand()/(double)RAND_MAX);
float surface(float x, float y) {
float pi=4.0*atan(1.0);
float mu1, mu2, sig1, sig2;
float a, b;
float z1, z2;
mu1=sqrt(2.0);
mu2=sqrt(pi);
sig1=3.1;
sig2=1.4;
z1=0.1*sin(x)*sin(x*y);
a=pow((x-mu1),2)/(2*pow(sig1,2));
b=pow((y-mu2),2)/(2*pow(sig2,2));
z2=exp(-(a+b))/(sig1*sig2*sqrt(2.0*pi));
return z1+z2;
}
int main(int argc, char **argv) {
float xval, yval, zval;
int nsamps;
if ( argc != 2 ) {
cout <<"Usage: number of samples to test\n";
return 1;
}
else {
nsamps=stoi(argv[1]);
}
// Define the parameters to test
float pi=4.0*atan(1.0);
float xlo=-10.*pi;
float xhi=10.*pi;
float ylo=-10.*pi;
float yhi=10.*pi;
srand(time(0));
float xmax=0.;
float ymax=0.;
float zmax=0.;
for (int i=0;i<nsamps;++i) {
for (int j=0;j<nsamps;++j) {
xval=xlo+(xhi-xlo)*urand;
yval=ylo+(yhi-ylo)*urand;
zval=surface(xval,yval);
if (zval>zmax) {
zmax=zval;
xmax=xval;
ymax=yval;
}
}
}
cout<<"Result is "<<zmax<<" at "<<xmax<<","<<ymax<<endl;
}
Fortran
module random
implicit none
! Author: Katherine Holcomb
! Shortened version of a longer module
! Module incorporated into this file for convenience; typically it would be in its
! own file.
! Comment out one or the other when the module is incorporated into a code.
! Single precision
integer, parameter :: rk = kind(1.0)
! Double precision
!integer, parameter :: rk = kind(1.0d0)
contains
subroutine set_random_seed(seed)
! Sets all elements of the seed array
integer, optional, intent(in) :: seed
integer :: isize
integer, dimension(:), allocatable :: iseed
integer, dimension(8) :: idate
integer :: icount, i
call random_seed(size=isize)
if ( .not. present(seed) ) then
call system_clock(icount)
allocate(iseed(isize),source=icount+370*[(i,i=0,isize-1)])
else
allocate(iseed(isize))
iseed=seed
endif
call random_seed(put=iseed)
end subroutine set_random_seed
function urand(lb,ub,seed)
! Returns a uniformly-distributed random number in the range lb to ub.
real(rk) :: urand
real(rk), optional, intent(in) :: lb,ub
real(rk), optional, intent(in) :: seed
integer :: iseed
real(rk) :: rnd
real(rk) :: lower,upper
if ( present(seed) ) then
iseed=int(seed)
call set_random_seed(iseed)
endif
if ( present(lb) ) then
lower=lb
else
lower=0.0_rk
endif
if ( present(ub) ) then
upper = ub
else
upper = 1.0_rk
endif
call random_number(rnd)
urand = lower+(upper-lower)*rnd
return
end function urand
end module
program find_max
use random
implicit none
real :: pi=4.0*atan(1.0)
real :: xlo, xhi, ylo, yhi
real :: zval, zmax
real xval, yval
real xmax, ymax
integer :: i, j, nargs
integer :: nsamps
integer :: max_xind, max_yind
character(len=12) :: n
interface
real function surface(x,y)
implicit none
real, intent(in) :: x, y
end function
end interface
nargs=command_argument_count()
if ( nargs .ne. 1 ) then
stop "Usage: number of samples to test"
else
call get_command_argument(1,n)
read(n,'(i12)') nsamps
endif
call set_random_seed()
! Define the parameters to test
xlo=-10.*pi; xhi=10.*pi
ylo=-10.*pi; yhi=10.*pi
!We would usually have a lot of x,y points so cannot create z as a function
!of x and y, so have to use a loop rather than intrinsics
max_xind=1
max_yind=1
xmax=0.
ymax=0.
zmax=0.
do i=1,nsamps
do j=1,nsamps
xval=urand(xlo,xhi)
yval=urand(ylo,yhi)
zval=surface(xval,yval)
if (zval>zmax) then
zmax=zval
xmax=xval
ymax=yval
endif
enddo
enddo
write(*,'(a,f0.6,a,f0.6,a,f0.6)') "Result is ",zmax," at x,y=",xmax,", ",ymax
end program
real function surface(x,y)
implicit none
real, intent(in) :: x, y
real :: pi=4.0*atan(1.0)
real :: mu1, mu2, sig1, sig2
real :: a, b
real :: z1, z2
mu1=sqrt(2.0)
mu2=sqrt(pi)
sig1=3.1
sig2=1.4
z1=0.1*sin(x)*sin(x*y)
a=(x-mu1)**2/(2*sig1**2)
b=(y-mu2)**2/(2*sig2**2)
z2=exp(-(a+b))/(sig1*sig2*sqrt(2.0*pi))
surface=z1+z2
end function
Python
import sys
import numpy as np
def surface(x,y):
"""This is the main processing function. We use a ufunc."""
mu1=np.sqrt(2.0)
mu2=np.sqrt(np.pi)
sig1=3.1
sig2=1.4
z1=0.1*np.sin(x)*np.sin(x*y)
a=(x-mu1)**2/(2*sig1**2)
b=(y-mu2)**2/(2*sig2**2)
z2=np.exp(-(a+b))/(sig1*sig2*np.sqrt(2.0*np.pi))
z=z1+z2
return z
if __name__ == '__main__':
if len(sys.argv)==2:
nsamps=int(float(sys.argv[1]))
else:
print("Usage: number of samples")
exit()
# Define the parameters to test
xlo=-10.*np.pi; xhi=10.*np.pi
ylo=-10.*np.pi; yhi=10.*np.pi
#We would usually have a lot of x,y points so cannot create z as a function
#of x and y, so have to use a loop
zmax=0.
for i in range(nsamps):
for j in range(nsamps):
xval=np.random.uniform(xlo,xhi)
yval=np.random.uniform(ylo,yhi)
zval=surface(xval,yval)
if zval>zmax:
zmax=zval
xmax=xval
ymax=yval
max_xind=i
max_yind=j
print(f"Result is {zmax:.4f} at x,y= {xmax:.4f},{ymax:.4f} ")
Example Solutions
C++
#include <iostream>
#include <iomanip>
#include <string>
#include <sstream>
#include <random>
#include <cmath>
#include "mpi.h"
using namespace std;
#define urand ((double)rand()/(double)RAND_MAX);
float surface(float x, float y) {
float pi=4.0*atan(1.0);
float mu1, mu2, sig1, sig2;
float a, b;
float z1, z2;
mu1=sqrt(2.0);
mu2=sqrt(pi);
sig1=3.1;
sig2=1.4;
z1=0.1*sin(x)*sin(x*y);
a=pow((x-mu1),2)/(2*pow(sig1,2));
b=pow((y-mu2),2)/(2*pow(sig2,2));
z2=exp(-(a+b))/(sig1*sig2*sqrt(2.0*pi));
return z1+z2;
}
int main(int argc, char **argv) {
float xval, yval, zval;
int nprocs, rank;
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &nprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
int nsamps;
bool shutdown=false;
if (rank==0) {
if ( argc != 2 ) {
cout <<"Usage: number of samples to test\n";
shutdown=true;
}
else {
nsamps=stoi(argv[1]);
}
}
MPI_Bcast(&shutdown,1,MPI_CXX_BOOL,0,MPI_COMM_WORLD);
if (shutdown) {
MPI_Finalize();
exit(1);
}
MPI_Bcast(&nsamps,1,MPI_INT,0,MPI_COMM_WORLD);
// Define the parameters to test
float pi=4.0*atan(1.0);
float xlo=-10.*pi;
float xhi=10.*pi;
float ylo=-10.*pi;
float yhi=10.*pi;
srand(time(0)+rank);
float xmax=0.;
float ymax=0.;
float zmax=0.;
for (int i=0;i<nsamps;++i) {
for (int j=0;j<nsamps;++j) {
xval=xlo+(xhi-xlo)*urand;
yval=ylo+(yhi-ylo)*urand;
zval=surface(xval,yval);
if (zval>zmax) {
zmax=zval;
xmax=xval;
ymax=yval;
}
}
}
float *xresult=new float[nprocs];
float *yresult=new float[nprocs];
float *zresult=new float[nprocs];
MPI_Gather(&xmax,1,MPI_FLOAT,xresult,1,MPI_FLOAT,0,MPI_COMM_WORLD);
MPI_Gather(&ymax,1,MPI_FLOAT,yresult,1,MPI_FLOAT,0,MPI_COMM_WORLD);
MPI_Gather(&zmax,1,MPI_FLOAT,zresult,1,MPI_FLOAT,0,MPI_COMM_WORLD);
if (rank==0) {
float g_zmax=zresult[0];
float g_xmax=xresult[0];
float g_ymax=yresult[0];
for (int i=1;i<nprocs;++i) {
if (zresult[i] > g_zmax) {
g_zmax=zresult[i];
g_xmax=xresult[i];
g_ymax=yresult[i];
}
}
cout<<"Result is "<<g_zmax<<" at x,y="<<g_xmax<<", "<<g_ymax<<endl;
}
MPI_Finalize();
}
Fortran
module random
implicit none
! Author: Katherine Holcomb
! Shortened version of a longer module
! Module incorporated into this file for convenience; typically it would be in its
! own file.
! Comment out one or the other when the module is incorporated into a code.
! Single precision
integer, parameter :: rk = kind(1.0)
! Double precision
!integer, parameter :: rk = kind(1.0d0)
contains
subroutine set_random_seed(seed)
! Sets all elements of the seed array
integer, optional, intent(in) :: seed
integer :: isize
integer, dimension(:), allocatable :: iseed
integer, dimension(8) :: idate
integer :: icount, i
call random_seed(size=isize)
if ( .not. present(seed) ) then
call system_clock(icount)
allocate(iseed(isize),source=icount+370*[(i,i=0,isize-1)])
else
allocate(iseed(isize))
iseed=seed
endif
call random_seed(put=iseed)
end subroutine set_random_seed
function urand(lb,ub,seed)
! Returns a uniformly-distributed random number in the range lb to ub.
real(rk) :: urand
real(rk), optional, intent(in) :: lb,ub
real(rk), optional, intent(in) :: seed
integer :: iseed
real(rk) :: rnd
real(rk) :: lower,upper
if ( present(seed) ) then
iseed=int(seed)
call set_random_seed(iseed)
endif
if ( present(lb) ) then
lower=lb
else
lower=0.0_rk
endif
if ( present(ub) ) then
upper = ub
else
upper = 1.0_rk
endif
call random_number(rnd)
urand = lower+(upper-lower)*rnd
return
end function urand
end module
program find_max
use random
use mpi
implicit none
real :: pi=4.0*atan(1.0)
real :: xlo, xhi, ylo, yhi
real :: my_xlo, my_xhi, my_ylo, my_yhi
real :: zval, zmax
real :: xval, xincr, xmax
real :: yval, yincr, ymax
real, dimension(:), allocatable :: xvals, yvals
real, dimension(:,:), allocatable :: zvals
integer :: i, j, nargs
integer :: nsamps
character(len=12) :: n
integer :: rank, nprocs, ierr
integer, dimension(:), allocatable:: seed
integer :: iseed, icount
integer, dimension(:), allocatable:: maxinds
real, dimension(:), allocatable:: xresult,yresult,zresult
real :: g_zmax
logical :: shutdown=.false.
interface
real function surface(x,y)
implicit none
real, intent(in) :: x, y
end function
end interface
call MPI_Init(ierr)
call MPI_Comm_rank(MPI_COMM_WORLD,rank,ierr)
call MPI_Comm_size(MPI_COMM_WORLD,nprocs,ierr)
if (rank==0) then
nargs=command_argument_count()
if ( nargs .ne. 1 ) then
shutdown=.true.
write(*,*) "Usage: number of samples to test"
else
call get_command_argument(1,n)
read(n,'(i12)') nsamps
endif
endif
call MPI_Bcast(shutdown,1,MPI_LOGICAL,0,MPI_COMM_WORLD,ierr)
if (shutdown) then
call MPI_Finalize(ierr)
stop
endif
call MPI_Bcast(nsamps,1,MPI_INTEGER,0,MPI_COMM_WORLD,ierr)
! Define the parameters to test
xlo=-10.*pi; xhi=10.*pi
ylo=-10.*pi; yhi=10.*pi
!For correct statistical properties, we set random seeds for each rank
call system_clock(icount)
iseed=icount+rank
call set_random_seed(iseed)
xmax=0.
ymax=0.
zmax=0.
do i=1,nsamps
do j=1,nsamps
xval=urand(xlo,xhi)
yval=urand(ylo,yhi)
zval=surface(xval,yval)
if (zval>zmax) then
zmax=zval
xmax=xval
ymax=yval
endif
enddo
enddo
! If not allgather, only root needs to allocate
if (rank==0) then
allocate(maxinds(nprocs))
allocate(xresult(nprocs),yresult(nprocs),zresult(nprocs))
endif
call MPI_Gather(xmax,1,MPI_REAL,xresult,1,MPI_REAL,0,MPI_COMM_WORLD,ierr)
call MPI_Gather(ymax,1,MPI_REAL,yresult,1,MPI_REAL,0,MPI_COMM_WORLD,ierr)
call MPI_Gather(zmax,1,MPI_REAL,zresult,1,MPI_REAL,0,MPI_COMM_WORLD,ierr)
if (rank==0) then
g_zmax=maxval(zresult)
maxinds=maxloc(zresult)
write(*,'(a,f0.6,a,f0.6,a,f0.6)') &
"Result is ",g_zmax," at x,y=",xresult(maxinds(1)),", ",yresult(maxinds(1))
endif
call MPI_Finalize(ierr)
end program
real function surface(x,y)
implicit none
real, intent(in) :: x, y
real :: pi=4.0*atan(1.0)
real :: mu1, mu2, sig1, sig2
real :: a, b
real :: z1, z2
mu1=sqrt(2.0)
mu2=sqrt(pi)
sig1=3.1
sig2=1.4
z1=0.1*sin(x)*sin(x*y)
a=(x-mu1)**2/(2*sig1**2)
b=(y-mu2)**2/(2*sig2**2)
z2=exp(-(a+b))/(sig1*sig2*sqrt(2.0*pi))
surface=z1+z2
end function
Python
from mpi4py import MPI
import numpy as np
import sys
def surface(x,y):
"""This is the main processing function. We use a ufunc for MPI."""
mu1=np.sqrt(2.0)
mu2=np.sqrt(np.pi)
sig1=3.1
sig2=1.4
z1=0.1*np.sin(x)*np.sin(x*y)
a=(x-mu1)**2/(2*sig1**2)
b=(y-mu2)**2/(2*sig2**2)
z2=np.exp(-(a+b))/(sig1*sig2*np.sqrt(2.0*np.pi))
z=z1+z2
return z
if __name__ == '__main__':
comm=MPI.COMM_WORLD
rank=comm.Get_rank()
nprocs=comm.Get_size()
shutdown=None
nsamps=0
if rank==0:
if len(sys.argv)==2:
nsamps=int(float(sys.argv[1]))
shutdown=False
else:
print("Usage: number of samples")
shutdown=True
shutdown=comm.bcast(shutdown,root=0)
if shutdown:
MPI.Finalize()
exit()
nsamps=comm.bcast(nsamps,root=0)
#Fairly crude effort to get different seeds on different processes
rng = np.random.default_rng()
my_nsamps=nsamps//nprocs
if nsamps%nprocs !=0:
#somewhat dopey load-balancing
remainder=nsamps%nprocs
for n in range(remainder):
if rank==n:
my_nsamps+=1
# Define the parameters to test
xlo=-10.*np.pi; xhi=10.*np.pi
ylo=-10.*np.pi; yhi=10.*np.pi
tic=MPI.Wtime()
#We would usually have a lot of x,y points so cannot create z as a function
#of x and y, so have to use a loop
zmax=0.
for i in range(nsamps):
for j in range(nsamps):
xval=rng.uniform(xlo,xhi)
yval=rng.uniform(ylo,yhi)
zval=surface(xval,yval)
if zval>zmax:
zmax=zval
xmax=xval
ymax=yval
max_xind=i
max_yind=j
my_xresult=np.array([xmax])
my_yresult=np.array([ymax])
my_zresult=np.array([zmax])
xresult=np.empty(nprocs)
yresult=np.empty(nprocs)
zresult=np.empty(nprocs)
comm.Gather([my_xresult,MPI.FLOAT],[xresult,MPI.FLOAT])
comm.Gather([my_yresult,MPI.FLOAT],[yresult,MPI.FLOAT])
comm.Gather([my_zresult,MPI.FLOAT],[zresult,MPI.FLOAT])
toc=MPI.Wtime()
if rank==0:
g_zmax=zresult.max()
maxind=np.argmax(zresult)
g_xmax=xresult[maxind]
g_ymax=yresult[maxind]
print(f"Result is {g_zmax:.4f} at x,y= {g_xmax:.4f},{g_ymax:.4f} ")
MPI.Finalize()